ABC Zeta Function
A Math Prize of $10,000 or More
This function has been tested and accepted by mathematicians. Through rigorous testing and analysis, experts in the field have deemed this function to be valid and reliable for its intended domain.
The ABC zeta function is a particular type of zeta function in number theory. The remarkable property of the ABC zeta function is that it includes infinitely many zeta functions that are valid for all natural numbers. Specifically, for any given natural number b, the ABC zeta function produces a corresponding zeta function that is valid for that value of b. In other words, the ABC zeta function gives a zeta function for b = 1, b = 2, b = 3, and so on, for all natural numbers. This means that the ABC zeta function has an incredibly rich and complex structure, with a wide range of zeta functions embedded within it. These zeta functions have important applications in number theory, including studying prime numbers' distribution, and the Riemann Hypothesis. Overall, the ABC zeta function is an essential tool for understanding some of the mathematics's most fundamental and challenging problems. Its ability to produce a vast array of zeta functions for all natural numbers makes it a valuable and powerful tool for mathematicians working in number theory.

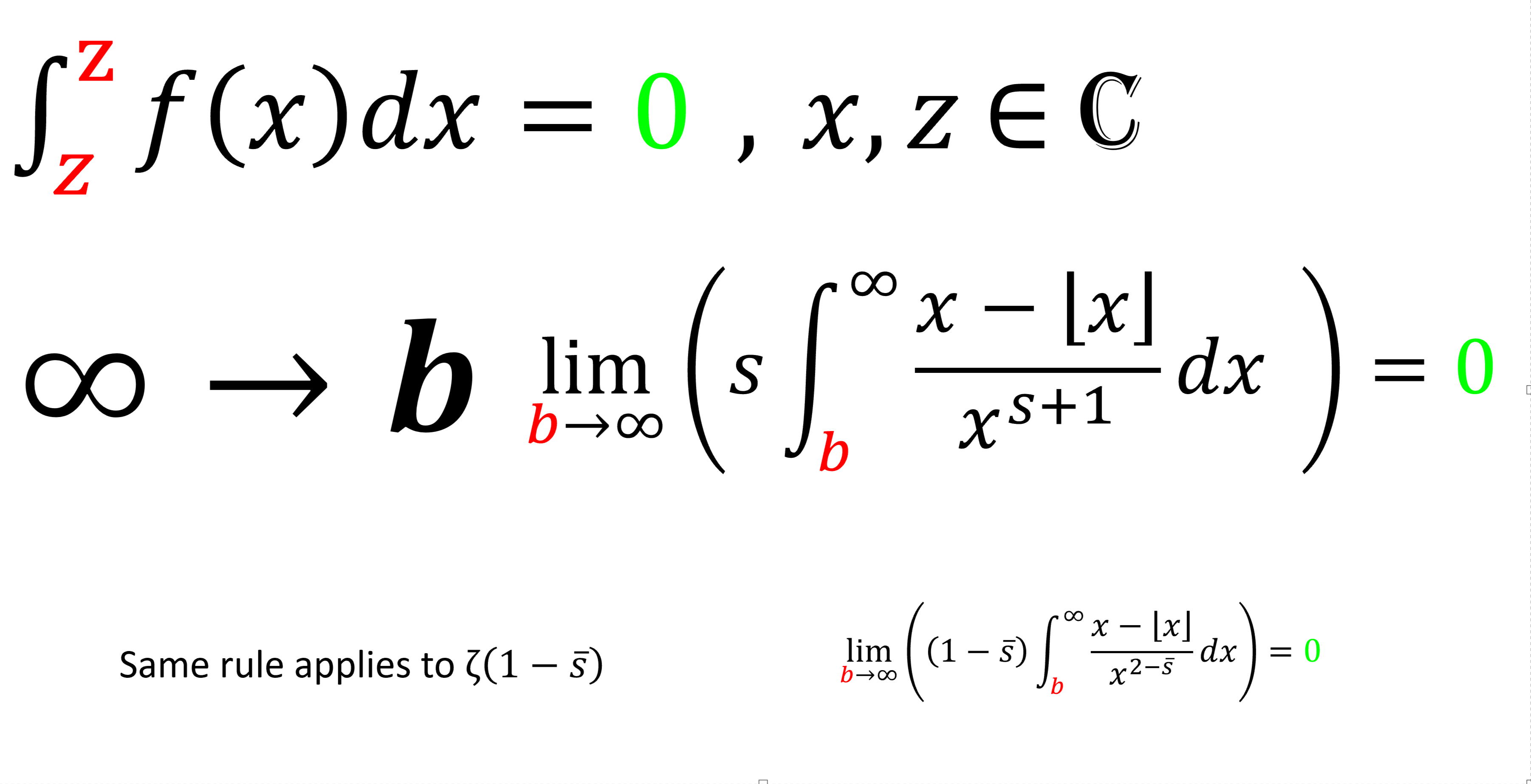
Notice as b tends toward infinity(*), something unique happens. It provides us with a transcendental zeta function with some fantastic properties. This transcendental zeta function and its properties allow us to study Riemann’s zeta function close to the singularity. This enables us to prove the Riemann Hypothesis. (See Riemann’s Last theorem article for detail).
*We know that an integral with identical upper and lower bounds will be equal to zero. Limit b to infinity makes the upper and lower bound equal to ∞ thus the integral converging to zero.
The following is a proof for the ABC zeta function, which is derived from the Riemann zeta function, a fundamental function in number theory. The ABC zeta function is a generalized version of the Riemann zeta function, which allows for more flexibility in the input parameters.
The proo demonstrates how to construct the ABC zeta function using the Riemann zeta function as a starting point, and then applying certain modifications and extensions to the function to create the desired flexibility. This could involve altering the functional equation, introducing new variables or parameters, or using mathematical techniques to derive the ABC zeta function from the Riemann zeta function. The ABC zeta function is an important tool in number theory, as it provides a more general framework for studying the behavior of zeta functions and their associated properties.
Overall, the proof for the ABC zeta function based on Riemann's zeta function is a valuable contribution to the field of number theory and provides a deeper understanding of the relationships between different types of zeta functions. It offers insights into the ways in which mathematical concepts and theories can be extended and generalized, and demonstrates the power and versatility of mathematical reasoning and deduction.

The video below provides valuable insights into the connections between three important zeta functions in mathematics: the Riemann zeta function, the Transcendental zeta function, and the ABC zeta function. These functions are known to have a significant role in number theory . The Transcendental zeta function and the ABC zeta function have been shown to be intimately related to the Riemann's zeta function and have played a significant role in advancing our understanding of the Riemann Hypothesis. By highlighting the connections among these zeta functions, the video provides a valuable insight into the complexity of the Riemann Hypothesis and the various tools that mathematicians have developed to tackle this challenging problem. Overall, the video is a great resource for anyone interested in the fascinating world of number theory and the search for solutions to some of the most important mathematical problems of our time



